Момент импульса является важной физической величиной, которая описывает вращательное движение тела. Закон сохранения момента импульса гласит, что момент импульса тела, находящегося в изолированной системе, сохраняется, если нет внешних моментов.
Формула для момента импульса выглядит следующим образом: L = Iω, где L — момент импульса, I — момент инерции тела и ω — угловая скорость вращения.
Закон сохранения момента импульса имеет широкое применение и объясняет множество явлений. Например, при вращении катания на роликах, спортсмен сжимает грузы к телу, чтобы увеличить свой момент инерции и замедлить вращение. Это объясняется законом сохранения момента импульса: сокращение момента инерции приводит к увеличению угловой скорости.
Закон сохранения момента импульса:
Момент импульса (L) определяется как произведение массы тела (m) на его линейную скорость (v) и его расстояние (r) от выбранной точки:
L = mvr
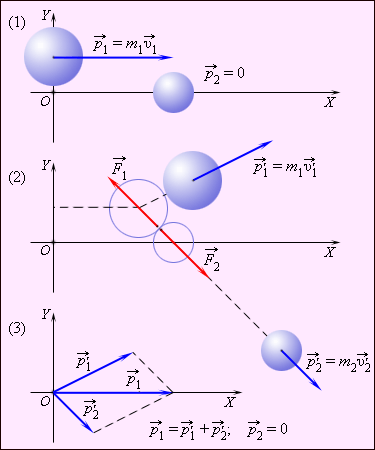
Если на систему не действуют внешние силы, то момент импульса остается постоянным. Это означает, что если одно тело передает свой импульс другому телу, то его момент импульса уменьшится, а момент импульса второго тела увеличится, так, чтобы их сумма оставалась неизменной.
Примером применения закона сохранения момента импульса является, например, движение фигуриста на льду. Когда фигурист совершает вращательные движения, его момент инерции увеличивается, что позволяет ему изменять скорость вращения. Если он желает увеличить свою скорость вращения, он сжимает свои конечности, что уменьшает его момент инерции, и наоборот.
Формула момента импульса
М = Iω
Где:
- М — момент импульса;
- I — момент инерции тела (величина, зависящая от распределения массы тела относительно оси вращения);
- ω — угловая скорость вращения тела.
Формула момента импульса позволяет вычислить эту величину для любого вращающегося тела, учитывая его массу, форму и скорость вращения.
Закон сохранения момента импульса гласит, что если на тело не действуют внешние моменты сил, то его момент импульса остается постоянным. То есть, если тело совершает вращательное движение без влияния внешних сил или вращается вокруг неподвижной оси, то его момент импульса сохраняется.
Знание формулы момента импульса позволяет ученным и исследователям анализировать и предсказывать поведение вращающихся объектов с точки зрения закона сохранения момента импульса.
Определение момента импульса
Для понимания определения момента импульса необходимо разъяснить некоторые понятия. Вращательное движение — это движение, при котором тело поворачивается вокруг оси. Отличие вращательного движения от поступательного состоит в том, что вращательное движение происходит не вдоль прямой линии, а вокруг оси вращения.
Моментом импульса называется величина, которая равна произведению массы тела на его угловую скорость и момент инерции тела. Угловая скорость определяет скорость вращения тела вокруг оси, а момент инерции характеризует его инерцию, то есть сопротивление изменению движения.
Математически момент импульса выражается следующей формулой:
| J = I * ω |
где J — момент импульса, I — момент инерции тела, ω — угловая скорость.
Определение момента импульса является важным для изучения вращательных движений и является одним из основных законов физики — закона сохранения момента импульса.
Формула момента импульса
Формула момента импульса выглядит следующим образом:
Где:
— момент импульса;
— масса тела;
— радиус-вектор, направленный от оси вращения до точки, в которой находится частица;
— скорость частицы.
Таким образом, формула момента импульса позволяет связать величину момента с параметрами тела и его движения. Его направление определяется по правилу правой руки, где указательный палец соответствует направлению радиус-вектора , а средний палец – направлению скорости
.
Примеры применения закона
Закон сохранения момента импульса применяется в различных областях науки и техники, где важно учитывать изменение момента импульса системы.
Один из классических примеров применения закона сохранения момента импульса — движение твёрдого тела вращения. Если на твёрдое тело вращения не действуют моменты сил, то его момент импульса остаётся постоянным. Это позволяет прогнозировать изменения положения и скорости вращения тела.
Пример из механики жидкости — вращение водяного колеса. Когда вода падает на лопасти колеса и вращает его, момент импульса системы сохраняется. Это позволяет использовать водяные колеса для получения механической энергии.
В астрономии закон сохранения момента импульса применяется при изучении движения планет и спутников. Если не учитывать внешние воздействия, то момент импульса системы, состоящей из планеты и спутника, остается постоянным.
| Область | Пример применения |
|---|---|
| Механика твёрдого тела | Движение твёрдого тела вращения |
| Механика жидкости | Вращение водяного колеса |
| Астрономия | Движение планет и спутников |
Столкновение тел с различными массами
Рассмотрим случай столкновения двух тел с массами m1 и m2, где m1 > m2. Пусть перед столкновением первое тело имело скорость v1, а второе тело – v2. По закону сохранения момента импульса:
m1 * v1 + m2 * v2 = m1 * v1′ + m2 * v2′
где v1′ и v2′ – скорости тел после столкновения. Если тела после столкновения остаются вместе и двигаются с общей скоростью v, то:
m1 * v1 + m2 * v2 = (m1 + m2) * v
Отсюда можно найти скорость v:
v = (m1 * v1 + m2 * v2) / (m1 + m2)
Пример: пусть m1 = 5 кг, m2 = 2 кг, v1 = 10 м/с, v2 = -5 м/с. Тогда скорость v после столкновения будет:
v = (5 * 10 + 2 * (-5)) / (5 + 2) = 7 м/с
Таким образом, при столкновении тел с различными массами закон сохранения момента импульса позволяет определить скорость тел после столкновения.
| Масса тела (кг) | Начальная скорость (м/с) | Конечная скорость (м/с) |
|---|---|---|
| m1 | v1 | v1′ |
| m2 | v2 | v2′ |
Вращение рычага с неизменной скоростью
Представьте себе рычаг, который вращается вокруг фиксированной оси. Если на рычаг действуют только нормальные силы, то его скорость вращения будет постоянной. В этом случае можно сказать, что момент сил, действующих на рычаг, сохраняется.
Скорость вращения рычага с неизменной скоростью можно объяснить с помощью закона сохранения момента импульса. Согласно этому закону, момент импульса системы остается постоянным, если на нее не действуют внешние моменты силы.
В случае вращения рычага с неизменной скоростью, момент импульса рычага в начальный момент времени равен моменту импульса рычага в конечный момент времени. Это означает, что скорость вращения рычага не изменяется со временем.
Это свойство вращения рычага с неизменной скоростью можно использовать в различных областях, например, в механике, при работе с механизмами и устройствами. Знание закона сохранения момента импульса даёт возможность предсказывать изменения скорости вращения рычага и делать соответствующие расчёты.
Объяснение закона сохранения момента импульса
Момент импульса — это векторная физическая величина, равная произведению массы тела на его скорость и расстояние до оси вращения.
Закон сохранения момента импульса можно объяснить на примере вращающегося тела. Представим, что у нас есть гиря, к которой приложено одно внешнее вращательное мгновенное действие силы. Если гиря свободно вращается, то ее момент импульса остается неизменным. Если на гирю воздействует еще одна сила, то ее момент импульса изменится.
Закон сохранения момента импульса имеет широкое применение в различных областях физики, включая механику, гидродинамику и астрономию. Его применение позволяет провести анализ и прогнозирование движения тел в системе и определить зависимость момента импульса от внешних сил.
Принцип сохранения момента импульса
Момент импульса – это векторная физическая величина, которая характеризует вращательное движение системы относительно выбранной оси. Он определяется как произведение момента инерции на угловую скорость:
$$\vec{L} = \mathbf{I} \cdot \vec{\omega}$$
Где:
- $$\vec{L}$$ – момент импульса системы,
- $$\mathbf{I}$$ – момент инерции системы,
- $$\vec{\omega}$$ – угловая скорость системы.
Принцип сохранения момента импульса можно интерпретировать следующим образом: если система находится в изолированном состоянии, то ее момент импульса не изменяется со временем. Это означает, что если одна часть системы начинает вращаться быстрее, то другая часть системы начнет вращаться медленнее, чтобы компенсировать изменение общего момента импульса.
Принцип сохранения момента импульса широко применяется в различных областях физики, включая механику, астрономию и молекулярную физику. Он помогает объяснить такие явления, как вращение планет вокруг своей оси, вращение спутников вокруг планеты и многое другое.
A
Рассмотрим пример вращающегося катапультируемого кресла. Когда человек находится в исходном положении на катапульте, его момент импульса равен нулю. Однако, когда катапульта запускает кресло в воздух, момент импульса начинает увеличиваться.
При этом, человек будет вращаться с некоторой угловой скоростью, а его момент инерции будет зависеть от распределения массы его тела относительно оси вращения. Если человек, например, вытянет ноги, его момент инерции увеличится, что приведет к увеличению момента импульса и увеличению угловой скорости вращения.
Из этого примера видно, как момент импульса сохраняется в системе, и как изменения в моменте инерции и угловой скорости влияют на его значение. Принцип сохранения момента импульса является фундаментальным законом при рассмотрении вращательного движения систем.
Вопрос-ответ:
Что такое закон сохранения момента импульса?
Закон сохранения момента импульса утверждает, что если на систему не действуют внешние моменты сил, то момент импульса этой системы остается постоянным со временем.
Какая формула закона сохранения момента импульса?
Формула закона сохранения момента импульса выглядит следующим образом: L = r × p, где L — момент импульса, r — радиус-вектор относительно некоторой точки, p — импульс.
Можете привести пример применения закона сохранения момента импульса?
Конкретным примером применения закона сохранения момента импульса является вращение фигуриста на льду. Когда фигурист сжимает руки к телу, его момент инерции уменьшается, и, согласно закону сохранения момента импульса, его угловая скорость должна увеличиться.
Как объяснить закон сохранения момента импульса?
Закон сохранения момента импульса можно объяснить на основе принципа сохранения энергии. Если на систему не действуют внешние моменты сил, то момент импульса системы не меняется, и, следовательно, энергия системы сохраняется.
Что происходит, если на систему действуют внешние моменты сил?
Если на систему действуют внешние моменты сил, то закон сохранения момента импульса не выполняется, и момент импульса системы может изменяться со временем.
Что такое закон сохранения момента импульса?
Закон сохранения момента импульса утверждает, что если на систему тел не действуют внешние моменты сил, то момент импульса этой системы остается постоянным со временем.