Закон 1 Кеплера — одно из основных открытий Иоганна Кеплера, немецкого астронома и математика XVI-XVII веков, которое легло в основу современной астрономии. Этот закон космической динамики называется законом орбит и гласит, что все планеты движутся по орбитам вокруг Солнца, придерживаясь эллиптической формы.
Закон Кеплера является первым из трех основных законов, описывающих движение планет в Солнечной системе. Он основан на наблюдательных данных, собранных Кеплером за многие годы о наблюдении планет, включая Марс. Кеплер установил, что орбиты планет являются эллиптическими, а Солнце находится в одном из фокусов эллипса.
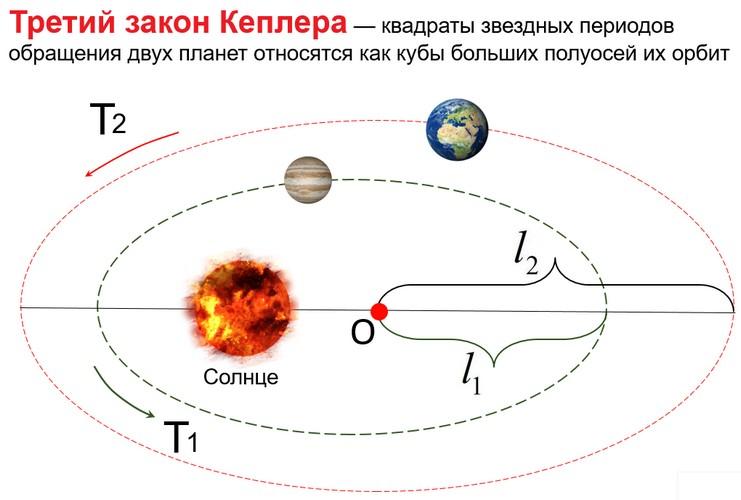
Формула, описывающая закон 1 Кеплера, имеет вид: T2 = k * R3, где T — период обращения планеты вокруг Солнца, R — большая полуось орбиты планеты, k — постоянная, зависящая от массы Солнца. Эта формула позволяет вычислить период обращения планеты вокруг Солнца по известному значению большой полуоси орбиты.
Примером применения закона 1 Кеплера может служить расчет периода обращения Земли вокруг Солнца. Известно, что большая полуось орбиты Земли составляет примерно 149,6 миллионов километров. Подставив это значение в формулу, можно вычислить, что период обращения Земли вокруг Солнца составляет примерно один год. Таким образом, закон 1 Кеплера позволяет описать и предсказать движение планет в Солнечной системе, а также провести необходимые расчеты.
Описание закона 1 Кеплера
Согласно закону Кеплера, планета движется вокруг Солнца по эллиптической орбите, а Солнце находится в одном из фокусов этой орбиты. Второй фокус находится внутри орбиты, но обычно он ближе к Солнцу. Полуось орбиты называется большой полуосью, обозначаемой символом «a». Расстояние от Солнца до планеты в разных точках орбиты меняется, и наибольшее расстояние называется афелием, а наименьшее — перигелием.
Закон 1 Кеплера объясняет, что планеты движутся по орбитам, более или менее эллиптическим, а не окружностям. Это открытие было сделано Кеплером на основе наблюдений и анализа данных, собранных его предшественником Тихо Браге.
Одним из примеров, подтверждающих закон 1 Кеплера, является орбита Земли вокруг Солнца. По орбите Земли Солнце располагается очень близко к одному из фокусов эллипса, создавая небольшую эллиптическую траекторию.
Ваш подзаголовок 1
Закон 1 Кеплера формулирует связь между орбитой планеты и Солнцем. Согласно этому закону, все планеты движутся по эллиптическим орбитам, одно из фокусов которых занимает Солнце.
Формула для Закона 1 Кеплера выглядит следующим образом:
r = a(1 — e),
где r — расстояние от планеты до Солнца, a — большая полуось орбиты планеты, e — эксцентриситет орбиты.
Например, пусть для определенной планеты a = 5 а.е. (астрономических единиц), а e = 0.2. Тогда расстояние от планеты до Солнца можно вычислить следующим образом:
r = 5(1 — 0.2) = 4 а.е.
Таким образом, Закон 1 Кеплера позволяет определить расстояние от планеты до Солнца, исходя из большой полуоси и эксцентриситета орбиты планеты.
Ваш подзаголовок 2
Закон 1 Кеплера, также известный как закон эллипсов, формулирует правило движения планет вокруг Солнца. Он гласит, что каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Формула закона 1 Кеплера выражается следующим образом:
| Формула закона | Описание |
|---|---|
| T^2 = K * r^3 | Период обращения планеты в квадрате равен постоянной Кеплера, умноженной на куб радиуса орбиты |
Здесь T обозначает период обращения планеты вокруг Солнца, r — радиус орбиты планеты относительно Солнца, а K — постоянная Кеплера.
Пример использования закона 1 Кеплера: Период обращения Земли вокруг Солнца составляет около 365,25 дней, а средний радиус орбиты Земли примерно 149,6 миллионов километров. Применяя формулу закона 1 Кеплера, мы можем вычислить значение постоянной Кеплера и использовать его для расчета периода обращения других планет вокруг Солнца.
Формула закона 1 кеплера
Закон 1 кеплера, также известный как закон орбит, описывает форму орбиты планет вокруг Солнца. Согласно этому закону, орбиты планет имеют форму эллипсов, где Солнце находится в одном из фокусов.
Формула, которая описывает закон 1 кеплера, выглядит следующим образом:
A: длина большой полуоси эллипса (афелия)
B: длина малой полуоси эллипса (перихелий)
e: эксцентриситет орбиты (0 < e < 1)
Формула: A × (1 — e) = B × (1 + e)
Эта формула позволяет вычислить длины полуосей эллипса по заданным значениям эксцентриситета.
Например, если дан эксцентриситет орбиты e = 0.5, то формула будет выглядеть следующим образом:
A × (1 — 0.5) = B × (1 + 0.5)
Таким образом, длина большой полуоси эллипса (афелия) будет в два раза больше длины малой полуоси эллипса (перихелий).
Формула закона 1 кеплера позволяет легко определить форму орбит планет и других небесных тел в Солнечной системе.
Ваш подзаголовок 3
Формула первого закона Кеплера выглядит следующим образом:
Орбита планеты является эллипсом, в одном из фокусов которого находится Солнце.
Примеры применения закона 1 Кеплера:
- Орбита Земли вокруг Солнца является эллипсом, где Солнце находится в одном из фокусов.
- Аналогично, орбиты других планет также являются эллипсами с Солнцем в одном из фокусов.
- Закон 1 Кеплера также применим к орбитам спутников вокруг планет и других небесных тел.
Примеры применения закона 1 кеплера
Закон 1 кеплера, также известный как закон орбит, гласит, что все планеты движутся по эллиптическим орбитам вокруг Солнца, при этом Солнце находится в одном из фокусов эллипса.
Применение этого закона можно увидеть в движении планет Солнечной системы. Например, Марс движется по эллиптической орбите вокруг Солнца. В этом случае Солнце находится в одном из фокусов эллипса, а Марс движется по этой орбите с постоянной скоростью.
Еще одним примером применения закона 1 кеплера является движение спутников вокруг планет. Например, Луна движется по эллиптической орбите вокруг Земли. Солнце находится в одном из фокусов этой орбиты, а Луна движется по ней, подвергаясь гравитационному притяжению Земли.
| Спутник | Орбита | Фокус | Скорость |
|---|---|---|---|
| Марс | Эллиптическая | Солнце | Постоянная |
| Луна | Эллиптическая | Солнце | Изменяющаяся |
Таким образом, закон 1 кеплера находит применение в изучении движения планет и спутников, позволяя определить форму и характеристики их орбит, а также исследовать гравитационные взаимодействия между небесными телами.
Ваш подзаголовок 4
Формулировка закона звучит следующим образом: «Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце».
Этот закон был открыт в 17 веке немецким астрономом Иоганном Кеплером.
Благодаря этому закону мы можем объяснить форму и особенности орбит планет в Солнечной системе. В результате применения закона Кеплера, было установлено, что орбиты планет имеют форму эллипса, но приближаются к окружности.
Примеры применения закона Кеплера можно найти не только в астрономии, но и в других областях науки. Например, движение комет вокруг Солнца также подчиняется закону Кеплера.
Ваш подзаголовок 5
Формула закона 1 кеплера выглядит следующим образом: а^2 = b^2 + c^2, где а – большая полуось эллипса, b – малая полуось эллипса, c – расстояние между Солнцем и фокусом эллипса.
Примером закона 1 кеплера может служить движение Земли вокруг Солнца. В этом случае эллипс, описываемый Землей, является ее орбитой. Солнце находится в одном из фокусов этого эллипса, а Земля движется по этой орбите, оставаясь всегда на определенном расстоянии от Солнца.
Вопрос-ответ:
Какую роль играет закон 1 кеплера в астрономии?
Закон 1 Кеплера является одним из основных законов в астрономии. Он описывает орбитальные движения планет вокруг Солнца и помогает понять их характеристики.
Какой формулой можно описать закон 1 Кеплера?
Формулой закона 1 Кеплера является следующее выражение: T^2 = k * R^3, где T — период обращения планеты вокруг Солнца, R — среднее расстояние между планетой и Солнцем, k — постоянная, которая зависит от единиц измерения.
Приведите пример применения закона 1 Кеплера.
Например, закон 1 Кеплера позволяет определить расстояние от Земли до Солнца. Зная период обращения Земли вокруг Солнца и используя формулу T^2 = k * R^3, можно получить значение среднего расстояния R.
Какую геометрическую форму имеют орбиты планет вокруг Солнца в соответствии с законом 1 Кеплера?
Согласно закону 1 Кеплера, орбиты планет имеют форму эллипсов, в одном из фокусов которых находится Солнце.
Какие единицы измерения используются в формуле закона 1 Кеплера?
В формуле закона 1 Кеплера используются следующие единицы измерения: период времени обращения планеты — в секундах или годах; расстояние между планетой и Солнцем — в метрах или астрономических единицах; постоянная k — зависит от выбранных единиц измерения и может быть различной.
Что такое закон 1 Кеплера?
Закон 1 Кеплера, также известный как закон движения планет, гласит, что орбиты планет имеют форму эллипсов, в одном из фокусов которых находится Солнце.
Какая формула используется для описания закона 1 Кеплера?
Для описания закона 1 Кеплера используется формула, определяющая эллипс: (x^2/a^2) + (y^2/b^2) = 1, где a и b — полуоси эллипса.